公益岗

今天，中公教育想要和大家分享的是行测考试当中数量关系的一类解题方法——比例。

比例指的是两种实际量的比值，比如某班级中男生和全班人数的比例为3：7，这就是一个比例关系，我们可以根据这个比例关系去计算求解。比例的核心是份数思想，也就是我们在利用比值时，其实可以把它们转化成份数去表示，我们刚才举的例子当中，就可以表示将班级总人数平均分成7份，将男生的人数平均分成3份。了解完这些之后，比例在实际应用当中，还需要具备一些基本能力，才能使我们如虎添翼，攻克难题，下面中公教育就和大家介绍比例基本能力中的比例化简。

比例的化简：比例在使用时，需要借助比值去进行求解，有时条件并没有直接告诉我们比值，而是需要我们通过条件的文字表述去转化，形成最终的比值，由于比值涉及到后期的计算，因此我们在化成比值时需将它们转化成最简比。

【例1】则甲、乙产品销量之比为?

【中公解析】结合条件等量关系可以列式为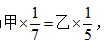若要让等式成立，可令等式两边都为1，即令甲为7，乙为5，则甲、乙产品销量之比为7：5。

注1：结合条件和结果可以发现甲、乙最终的比值为其对应相乘分数的分母，可得出所乘分数的分母为自己的。

【例2】甲产品销量的3倍与乙产品销量的4倍相等，则甲、乙产品销量之比为?

【中公解析】结合条件等量关系可以列式为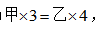若要让等式成立，可让左右两边结果为3和4的最小公倍数，即12，也就是令甲为4，乙为3，则甲、乙产品销量之比为4：3。

注2：若将3和4写成分数形式，在结合等量关系去列式，可得可以发现甲、乙最终的比值为另一个量所乘分数的分子，可得另一个数所乘分子为自己的，也就是自己所乘分数的分子是别人的。

结合例1和例2的结论，对于比例的统一时，我们可以借助一个口诀来快速找到他们的比例关系：分子是别人的，分母是自己的。

【例3】甲产品销量的则甲、乙产品销量之比为?

【中公解析】结合口诀，属于甲的有它的分数的分母7和乙的分数的分子4，属于乙的有它的分数的分母5和甲的分数的分子3，我们将所得的分母和分子相乘，即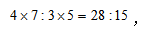则可知甲、乙产品销量之比为28：15.

以上就是今天中公教育想和大家分享的比例的统一，相信通过今天的学习，大家都能够快速的判断出条件所给的比例关系。行测考试注重平时的积累与应用，大家在学习完知识之后一定要结合题目去练习，才能够巩固知识，灵活运用。